Density Curriculum

Section 2—Lesson 4: How Can We Calculate Density From The Relationship Between Mass and Volume?

Lesson Plan

Materials

Prep Step

Explore Causality

Step 1: Analyzing What Happens to the Relationship Between Mass and Volume with the Same Substance

Remind the students about the patterns in terms of Relational Causality and density that they found in the last lesson; how when volume increased, so did mass.

The students learned that the relationship between mass and volume is constant for a pure substance under standard conditions. The relationship between the mass and the volume of any specimen has the same relationship.

Step 2: Analyzing What Happens to the Relationship Between Mass and Volume with Different Substances in Terms of Relational Causality and Density

Note to Teachers: The numbers for volume and mass below will need to be modified based on your actual samples. Replace these examples with your smallest sample and two larger samples.

Explain to your students that the relationship between mass and volume works in the same relational way to define or "cause" density. Use examples from the samples that they tested in this lesson.

If we show the relationship with the smallest sample of aluminum, it would look like this:

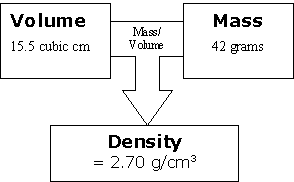
Volume-Mass-Density Relationship, Sample 1

Then take our second sample. We increase the volume and because it is the same substance, we increase the mass by the same number of units at the same time.

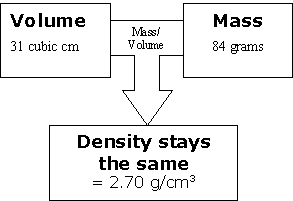
Volume-Mass-Density Relationship, Sample 2

The same thing happened with our third sample. Again, we increase the volume and because it is the same substance, we increase the mass by the same number of units at the same time.

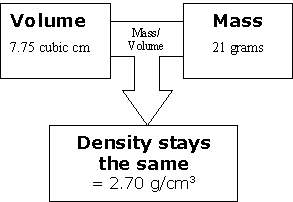
Volume-Mass-Density Relationship, Sample 3

Discuss the ideas just presented and see what questions students have. Encourage them to think about how this relationship changes when you compare different types of materials. Imagine that you have one material:

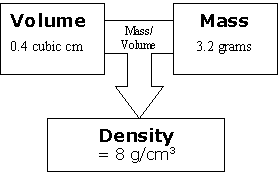
Volume-Mass-Density Relationship, Sample 4

Even though one thing alone can't cause the outcome, if you change one side of the relationship, the outcome changes. This is because it changes the relationship (just like with sisters). It doesn't matter which side you change, because it is the relationship between them that matters.

Ask your students, "Imagine that we have the same amount of volume, but more mass. This means more stuff has to fit in the same amount of space, so the density will do what?" [Go up.]

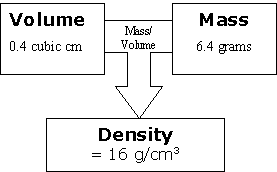
Volume-Mass-Density Relationship, Sample 5

Ask, "IImagine we have the same amount of mass but more volume. This means more space for the stuff to take up, so the density will do what?"I [Go down.]

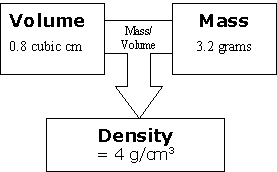
Volume-Mass-Density Relationship, Sample 6

Review, Extend, Apply

Step 3: Calculating Density from Mass and Volume

The students may have noticed that there are numbers attached to the density connected with each relationship between mass and volume. Introduce the concept of calculating density, being sure to present it as a relationship between the mass and the volume of an object.

Remind the students that they have been examining the relationship between mass and volume in order to talk about density. Density is a calculation of how much matter is squeezed into a given amount of space. It is a ratio—the amount of mass per unit of volume. Scientists define density as the mass of a substance per unit volume. It is the relationship between the mass (or weight) of one unit of a material and the volume of that one unit. Density is given in units of grams per cubic centimeter (g/cm3) or grams per milliliter (g/ml).

Explain that if you know the mass and volume of an object, you can figure out its density by dividing the mass by the volume (D = M/V). Explain that you will use a Dots-Per-Box Model to illustrate the concept of dividing the amount of matter by the amount of space. Draw the following model on the board:

Dots-Per-Box Model
Dots-Per-Box Model

Density describes how much stuff is in how much space. In this Dots-Per-Box Model, for instance, we can think of the dots as stuff, or mass, and the boxes as space, or volume. There are 18 dots, or grams, in 6 boxes, or centimeters. We can divide the amount of matter by the amount of space to get the density: 3 dots per box, or 3 grams per centimeter.

Of course the space is actually 3-dimensional not 2-dimensional, so this is one way that the Dots-Per-Box Model doesn't fit perfectly. For calculating density, we use cubic centimeters, not centimeters. Another way that the Dots-Per-Box Model doesn't fit exactly is that we can't know the mass of each dot of matter.

Step 4: Introducing Formulas for Calculating Density

Introduce the three formulas:

1) If you know the mass and volume of an object or substance, you can figure out its density by dividing the mass by the volume (D = M/V).

2) If you know the density and the volume of an object or substance, you can figure out its mass by multiplying the density times the volume (M = D x V).

3) If you know the density and mass of an object or substance, you can figure out its volume by dividing the mass by the density (V = M/D).

Tell the students that it can be difficult to directly memorize three formulas that are different, but similar in many respects. However, there is no reason to memorize all three formulas. If they understand that density is just the amount of matter for a given amount of space, then they can easily figure out the formulas.

Step 5: Demonstrating the Formulas

Show students how density is calculated using the following examples. There is a sheet entitled, Calculating Density included in case you would like the students to calculate these examples on their own first.

  • 4 cubic centimeters of a mystery substance has a mass of 3.2 grams. What is the density? [0.8 g/cm3]
  • A diamond with a volume of 2 cubic centimeters has a mass of 7 grams. What is its density? [3.5 g/cm3]
  • The density of cork is 0.2 g per cm3. If I have a cork with a mass of 0.4, what would its volume be? [2 cm3]
  • The density of steel is 7.8 g/cm3. If you have a steel cube that has a volume of 10 cm3, what is its mass? [78 g]

Step 6: Practice Using the Relationship Between Mass, Volume, and Density to Calculate the Unknown Variable

Hand out the sheet entitled, Practice Using the Relationship Between Mass, Volume, and Density to Calculate the Unknown Variable. This sheet is designed for students to practice calculating the density of solids. Circulate while your students are working to make sure that they understand the mathematical aspects of calculating density.

Step 7: A Discussion: Can You "Measure" Density?

Pose the following question to the students:

Some textbooks say, "The density of a solid can be measured..." What do you think about the word "measured"?

Engage the students on a discussion of whether or not this is a good word choice. Can density be directly measured? Help the students to realize that density can be figured out or calculated, but it can't be directly measured. This reinforces the idea that density is a relationship and that it is an intensive quantity.