Density Curriculum

Section 2—Lesson 3: What Patterns Can Be Found Between Mass, Volume, and Density?

Lesson Plan

Materials

Prep Step

Analyze Thinking

Step 1: Finding the Relationship between the Mass and Volume of Pure Substances

Remind the students that they have been looking at how two objects with the same volume can have different mass and that they have been developing models to help explain what is going on. The concept of density was introduced in the previous two lessons.

This lesson explores what happens with the density when you have different amounts of the same material. In previous lessons, we investigated what happened when we had the same amounts of different materials. Now we will examine different amounts of the same material.

Divide the class into working groups of approximately four students. Give each group of students one of the set of five or six samples of one pure substance (copper, aluminum, or steel, for instance). Ask them to make some observations about the volume and felt weight (in lieu of mass since they are not using the balance yet) of the samples. Ask them to make some predictions about the density of the samples.

Have them choose two of the samples and draw models of each showing what they think they would see if they had microscopic eyes as they did in lesson one. Circulate while students are working to gather a sense of their ideas.

Explore Outcomes

Step 2: Finding the Relationship Between Mass and Volume of Pure Substances

Explain to your students that they are going to explore the relationship between mass and volume for the various samples. First, they need to find out the mass and volume of each sample. Remind your students how to find the mass of a sample using the pan balance and gram masses (see related Sidebar: Finding the Mass of an Object - PDF 159 KB). Remind them how they can find the volume of regular and irregular objects (see related Sidebar: Finding the Volume of an Object - PDF 162 KB).

Pass out the sheet, Finding and Graphing Mass and Volume of Pure Substances. Have the students measure the mass and volume of various samples of a pure substance and plot their results on a graph.

After the students have done one sample of the substance, have them work on a second sample by trading with another group that has a different sample of the same substance (see Example of Graphing the Densities of Copper and Aluminum - PDF 170 KB and Examples of Graphing the Densities of Brass and Aluminum - PDF 343 KB).

Step 3: Analyzing the Patterns Between Mass and Volume

Have the students plot their data points on a class chart (either drawn on paper or a transparency of the graph sheet) for the materials they have measured. What patterns do they notice?

After each group has plotted their examples, ask the students what they have learned. Write their ideas on the board and ask what conclusions can be drawn. Ask them to interpret directly from the graph. What big messages does this activity tell them about density?

The students should notice that the relationship between mass and volume is constant for a pure substance under standard conditions. The graph should show a straight line. This is the graphic equivalent of saying that the relationship is constant and also the "pattern."

This relationship can be calculated and expressed as a number, and we will use mathematical formulas to represent the relationship and to calculate densities in the next lesson.

CHECKING IN

Ask the students to stop for a few moments and ask themselves the following questions:

1) Am I PUSHING my thinking to explore the concepts deeply? (If a concept is hard, am I not giving up but trying to think it through?)

2) Am I thinking carefully about what my classmates are saying?

3) Am I working "minds-on"—actively thinking about the patterns—instead of just letting my classmates answer?

Explore Causality

Step 4: Introducing Relational Causality

The graph that the students created shows that there is a relationship between the mass and the volume of an object—as one increases, so does the other at a constant rate for each increase for each type of substance. Density is defined by the relationship between mass and volume. It involves thinking about Relational Causality—the idea that something is caused or defined by a relationship—instead of the simpler idea that one thing causes or defines another thing.

Explain to your students that they are going to look at a social example to help them think about Relational Causality. Say, "Two girls, Sarah and Abby, can be sisters, but neither girl alone is the 'cause' of being sisters. It is the relationship between the two that 'causes' them to be sisters."

"You can make comparisons about the relationship. For example, you can say that one sister is older and one is younger but it only makes sense in terms of the relationship, in comparison to each other. So you can see that it if one thing changes so does the outcome."

Draw the following diagram on the board:

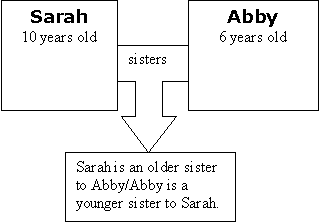
Sarah and Abby relationship

Explain to your students that if you change one part of the relationship, the outcome changes. You can't change your age, of course, so we need to change one of the "things" entirely. Show this in the diagram.

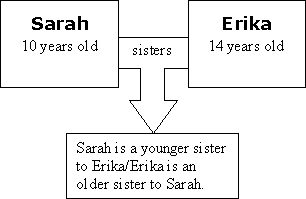
Sarah and Erika relationship

Hand out and discuss the sheet, What is Relational Causality?. You can also have the students work through the sheet entitled, Mapping Relational Causality: Density. (Students should fill "mass" into one of the top boxes and "volume" into the other top box and "density" into the bottom box.) You can also have your students read the sheet, Mapping Simple Linear Causality. This sheet offers a contrast to help them better grasp Relational Causality.

Step 5: Revisiting and Revising Our Models of What is Going On

Ask the students to think about what is going on in terms of models. Have them revisit their models from earlier lessons in the class. How would they revise them?

Which models do they think do the best job showing that each one-unit change in volume results in a specific change in mass for each type of substance? Models that unitize the amount of matter per volume such as "Dots-Per-Box Models" do an especially good job of illustrating what is going on when you go from a smaller to a larger sample of the same substance.